Kademlia using for discovery task in Ethereum Networking layer, to understand How Ethereum networking work, Kademlia is require.

Kademlia provides a way for millions of computers to self-organize into a network, communicate with other computers on the network, and share resources (e.g. files, blobs, objects) between computers, all without a central registry or lookup run by a single person or company

The cool thing is the finding complexity is O(log₂(n/k)) with n is number of network nodes, k is bucket size (describe below). For example network contain 10.000.000 nodes and bucket size is 4, it's only take log₂(10.000.000/4) ~= 21 times look ups.

Getting Started

Distributed Hash Table (DHT)

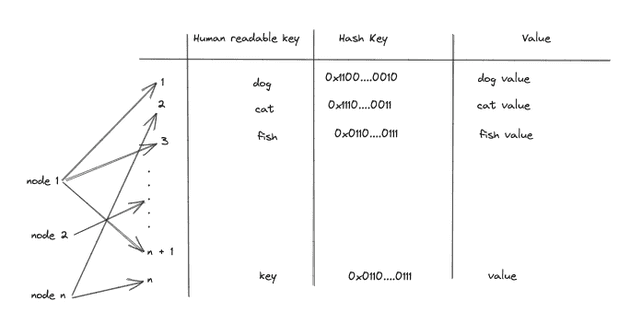
DHT is a distributed system that provides a lookup service similar to a hash table. Key–value pairs are stored in a DHT, and any participating node can efficiently retrieve the value associated with a given key.

Example of global hash table:

• The key space is for example 2^10 for using 10-bit key
• The number of node could be massive for single machine store, one individual node store same node, at least one node for connected to network so why is call "distributed"

There are 2 question here:

1. The rule for node identified what other node it should store for its local table?
2. If node want to find non-exist other node How could it find them?

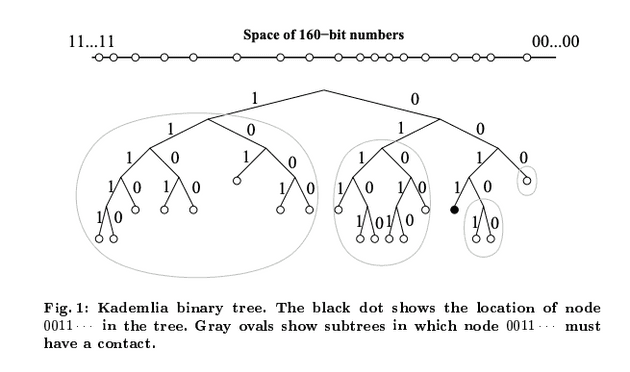
Kademlia Overview

• Kademlia takes the same general approach as other DTHs.
• Kademlia using 160-bit for node id.
• Kademlia treats nodes as leaves in binary tree, with each nodes's position determined by the shortest prefix of its ID

System describe

Kademlia node

• Kademlia node has a 160-bit NodeID (SHA-1) and IP Address, UDP port

Distance space

• This 'closeness' is not geographical - distance is defined by the similarity of the node's ID throw XOR operator. For example node 1: 0011 and node 2: 0001 distance is 0011 XOR 0001 = 2

The node state

The global state

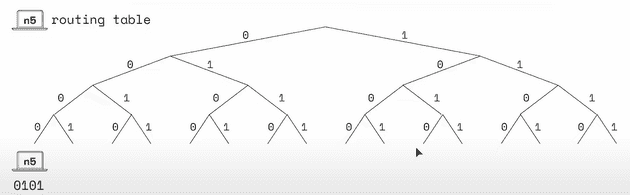
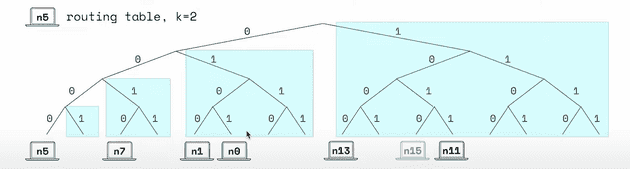
Here minimal version of kademlia with key space 4 bit (2^4 = 16 nodes) and k-bucket = 4. The global state should like below but keep in mind that's machine only store some node of global state.

The node state

• n5 has node id 0101 but start at path 0-0-0-0 because distance between it's self is 0 (0101 XOR 0101 is 0)

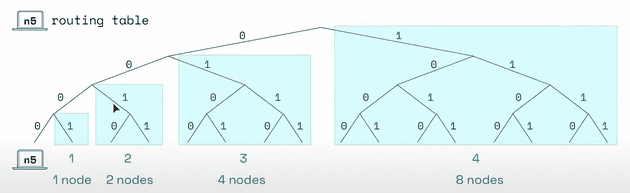
• k-bucket with k = 4 that's mean the remaining nodes divide 4 groups. The keys the buckets are equal to the number of width but also covering more space and more distance

• each bucket contain maximum 2 node, n-15 will not being added because we already have n13 and n11

Look up

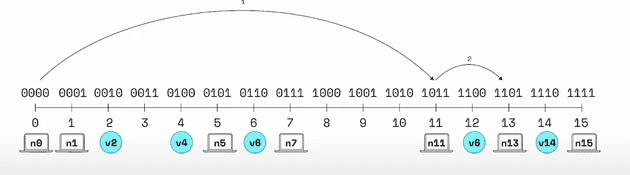
• n0 want to know information of v14
• n0 only store bucket-1 (n1), bucket-3 (n5, n7), bucket-4 (n1)
• n11 not store n14 but store n13

The progress will be:

1. n14 at bucket-4 of n0, so n0 ask closest node at bucket-4 is n11
2. n11 ask closest node at bucket-2 is n13
3. n13 will return n14 value

So because each node store its k-bucket itself so the maximum complexity will be O(log₂(n/k))

Reference

1. A Brief Overview of Kademlia, and its use in various decentralized platforms
2. Kademlia Paper
3. Kademlia Explain Videos